GeckoBot: A Gecko Inspired Incline-Climbing Robot
Vertical wall climbing robots have been a subject of scientific research for several years and could be used in a variety of applications. Robots that climb could eliminate the need for scaffolding when fulfilling jobs such as inspecting and maintaining airplanes and relieve humans of hazardous tasks such as window-washing and firefighting. An important consideration when designing these robots is its method for adhering to surfaces; consequently, researchers have identified and implemented different mechanisms for adhesion, including magnetic, pneumatic, electrostatic, and bio-inspired methods. Frequently, researchers have borrowed from the gecko’s unique method for adhesion when designing wall-climbing robots. Our project objective was to measure the effectiveness of a commonly used gecko-inspired adhesive in imparting wall climbing capabilities to a locomoting robot. Originally, we had planned to test our custom manufactured adhesive on a vertical wall; however, due to a lack of access to microfabrication techniques, we were forced to narrow our testing to inclined walls, and instead chose to measure the maximum incline our robot could climb without slipping thanks to the gecko-inspired adhesive feet.
Gecko’s Method for Adhesion
The remarkable climbing ability of the gecko has been attributed primarily to the tiny, hair-like structures found on the toes. The toes hold modified keratinized scales called lamellae which are subdivided into tiny, hair-like structures called setae. These structures are composed of several nanoscale-sized spatulae which provide high adhesion and friction forces between the toe pads and surfaces through van der Waals forces [1]. Figure 1 shows the hierarchical structure of the gecko and the forces that act on its components.
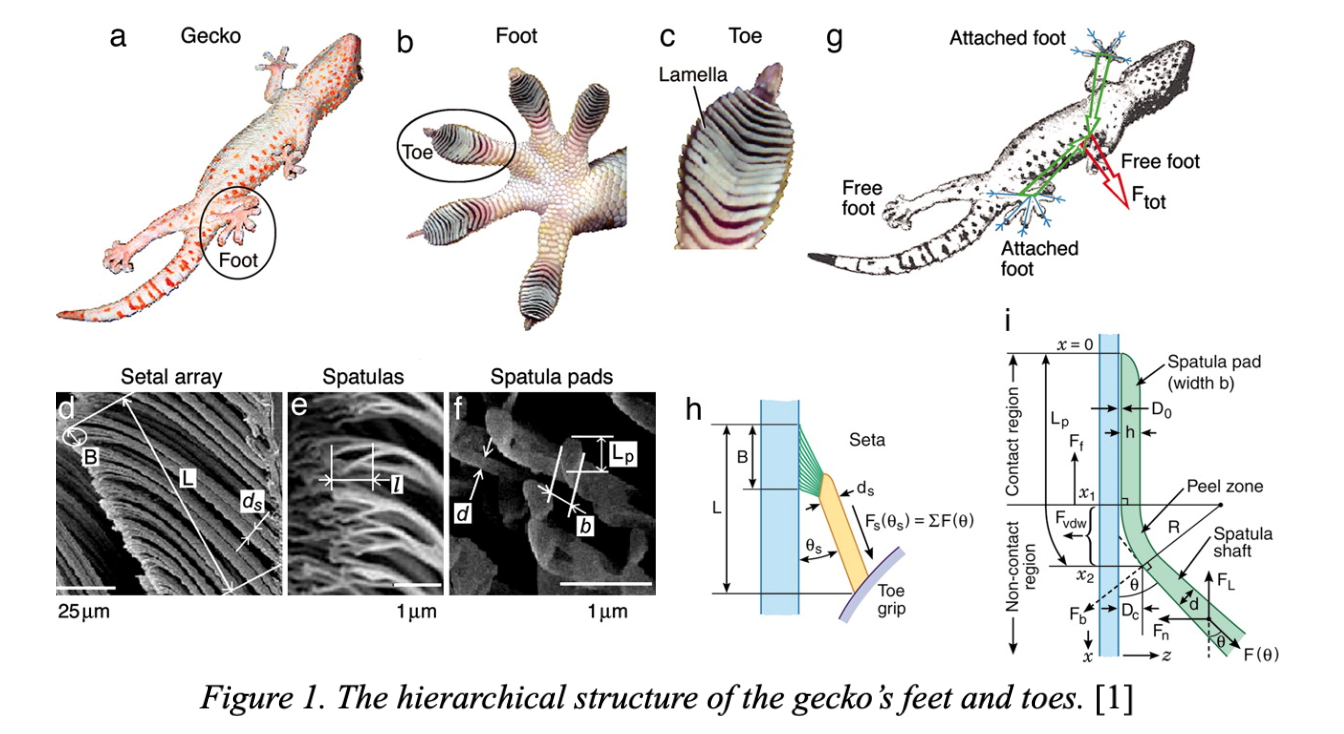
Figure 1-i illustrates the forces acting on a single spatula when the gecko is adhered to the wall. The lateral friction force \( F_L \) and normal adhesion force \( F_N \) act on each spatula during adhesion. Furthermore, the angle that varies the net force acting on each spatula, \( F(\theta) \), is often less than 45°. Therefore, the lateral friction force that acts on the spatula contributes non-negligibly to the gecko’s ability to not slip against the wall. The equation for \( F(\theta) \) is:
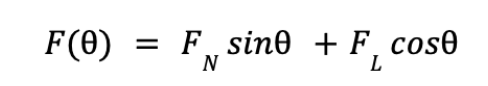
Researchers have employed MENS/NENS fabrication techniques, including photolithography, micro-molding, and plasma etching to manufacture pads with structures that emulate geckos’ setae [2,3].
Design Discussion
We began the project by designing a locomoting robot that could emulate the gecko’s locomotive climbing cycle and avoid pitch-back as it climbs up a wall. The robot would have four legs, and each leg had two degrees of freedom to replicate a gecko’s limb. One degree of freedom allowed abduction and adduction of each leg for the robot to move forward and lift itself up the surface. The other degree of freedom provided flexion and extension of each leg allowing the robot to adhere to and peel away from the wall. We chose to use eight servos to drive these movements because of their ability to precisely control the rotation of their motor shaft. The maximum mass of the robot would be 0.7 kg (W ~ 7N). The body and legs were made out of PLA to minimize the robot’s weight.
Force Analysis for Servo Selection
We carried out static force analysis to select the optimal dimensions of the robot and aid in motor selection. Since we planned on using 55g servos, we couldn’t neglect the weight of the linkages. Hence, we first found the equivalent CG of the entire robot in neutral position as such:
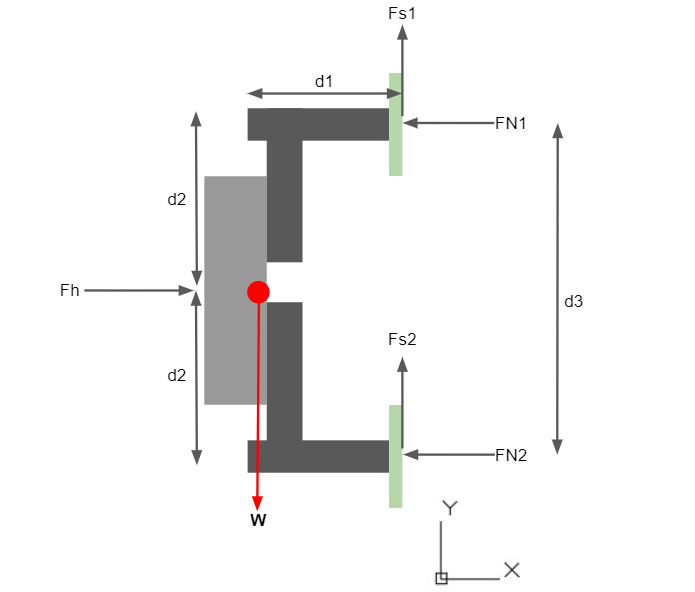
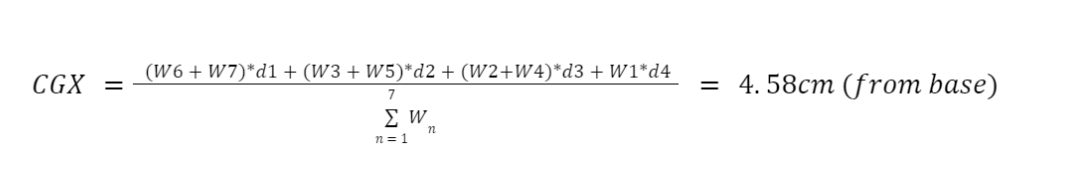
Since the robot is symmetric about the X axis, the Y coordinate of the CG can be found using CAD at 9cm from the back foot base. Thus, knowing the location of the CG in neutral position, we can label the minimum required adhesion and normal forces while the robot is in the "resting" position- all legs neutral, feet against a vertical surface. Seeing Fig [3], d1 is the distance between the robot’s center of mass and the wall, d2 is the distance between the CG and the middle of the first foot, and d3 is the distance between the centers of the two feet. Once again, only half of the robot weight is considered due to symmetry. Considering the robot to be in equilibrium at this moment, we find:
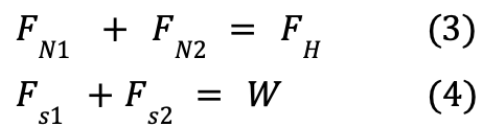
Moreover, since the robot is not slipping, the moments about the two feet centers and the CG balance out as:
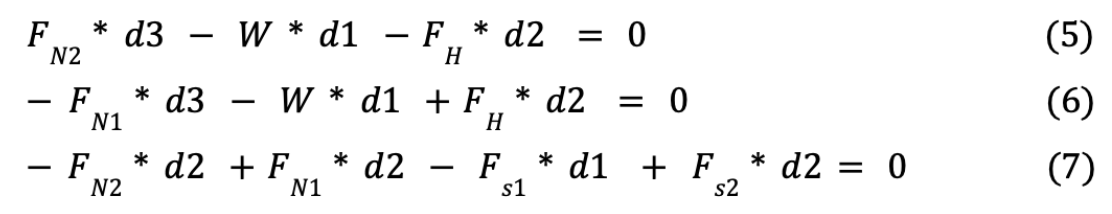
From this moment balance, we see that:
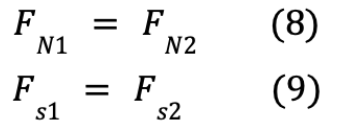
Equations (8) and (9) can also be found from the symmetry consideration of the robot. Finally, rearranging equation 7 yields the required horizontal force:
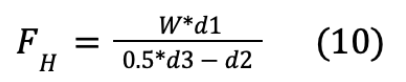
Given the designed values of d1, d2, and d3, we find the need for a horizontal force acting towards the surface of roughly 30% of the half weight of the robot. This is usually achieved in industry using vacuum suction cups. We also find the upwards shear forces on each pad to be 25% of the full robot weight, which is expected from the neutral position. Hence we find the resting torque required from each leg servo as T = FL, where L is the length of the linkage. For the foot servos, the torque can be easily found as Tf = GL, where L is again the length of the linkage and G is the weight of each foot in Newtons.
Silicone Pad design and Adhesive force test
Once we knew of the forces required from the servos, we moved on to finalize the form factor and design of the silicone pads. Our choice of silicone epoxy came from a previous project based on the research of Autumn et al[11] into synthetic materials that can mimic the unique properties of gecko feet. While conventional Pressure Sensitive Adhesives (PSAs) like duct tape or sticky note glue work on pure adhesion, the setae on gecko pads are an anisotropic frictional adhesive that require a proximally directed shear frictional force to maintain adhesion to the desired surface (Autumn et al, 2008). Each gecko foot has over 200,000 setae per toe, each of which provide an adhesive force that is directionally dependent on the angle of contact between the setae and the surface of interest. To create our gecko inspired adhesive, we used a polydimethylsiloxane (PMDS) and initially tried to replicate the features of a lamella. We used acrylic laser cutting as a manufacturing method to create molds with various different shapes of lamellae cut out, including circles of varying diameters, flanges, and even molds with no lamellae. The objective was to measure the adhesive force of each design and finally implement the design providing the highest adhesive force. In order to test the shear v/s adhesive force of each pad design, we planned to first adhere the pads to a vertical surface by providing a horizontal pushing force, and then begin attaching weights of increasing denominations to the pads and measure the maximum weight it was able to take without slipping. During the test, we realized the inefficiencies of our manufacturing methods- despite using the smallest allowable thickness settings of the laser cutter (0.1mm), the lamellae we created were too thick and were hence unable to bend as required to adhere to the vertical surface without the application of a significant horizontal force. Upon further research, we saw that lamellae used to replicate gecko adhesives have micron diameters, which we could not manufacture due a lack of microfabrication techniques. Moreover, the horizontal force would be in addition to that calculated in the previous section, and we realized that without additional mechanisms- like suction cups- it would be impossible for the robot to generate such high forces. In an attempt to reduce the weight and complexity of the project, we opted out of using additional force producing designs, and hence chose to forgo implementing lamellae and went with plain pads as they performed the best during adhesion testing. We also chose to modify the scope of the project to climb an inclined surface and measure the maximum incline the robot could climb without slipping, as climbing a perfectly vertical wall would be impossible without additional horizontal force. During testing, we saw that each 2x2inch plain PMDS pad was capable of handling 170g at 71 degrees and 250g at 47 degrees without slipping. Since our robot was estimated to weigh ~715g, we expected our maximum incline to be 61 degrees from horizontal.
Robot’s Locomotive Cycle
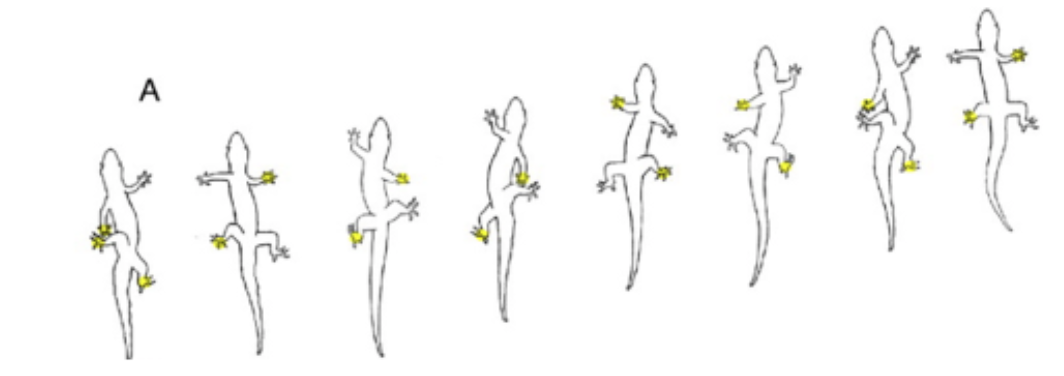
With resting servo forces calculated and silicone pad form factors decided, we moved on to creating the locomotive cycle of the robot that would then be implemented using the on board Arduino and a PWM servo controller. Each foot servo was used to lift feet off the ground and make ground contact, and the leg servos were used to swing the robot back and forth. Our locomotive cycle was based on the diagonal gait used by many researchers, which uses two diagonal legs to support the robot's body as it moves. In this gait, two diagonal legs extend forward and then pull the robot back, and by oscillating between the right diagonal and left diagonal legs, the robot lopes its way forward. This gait is inherently unstable because of the constant shift in CG due to the extension of only two legs at a time. Gecko's- and other industrial robots- overcome this CG shift by using CG correcting appendages like tails, and by fluidly twisting the torso to maintain CG along the path, as seen in the figures below.
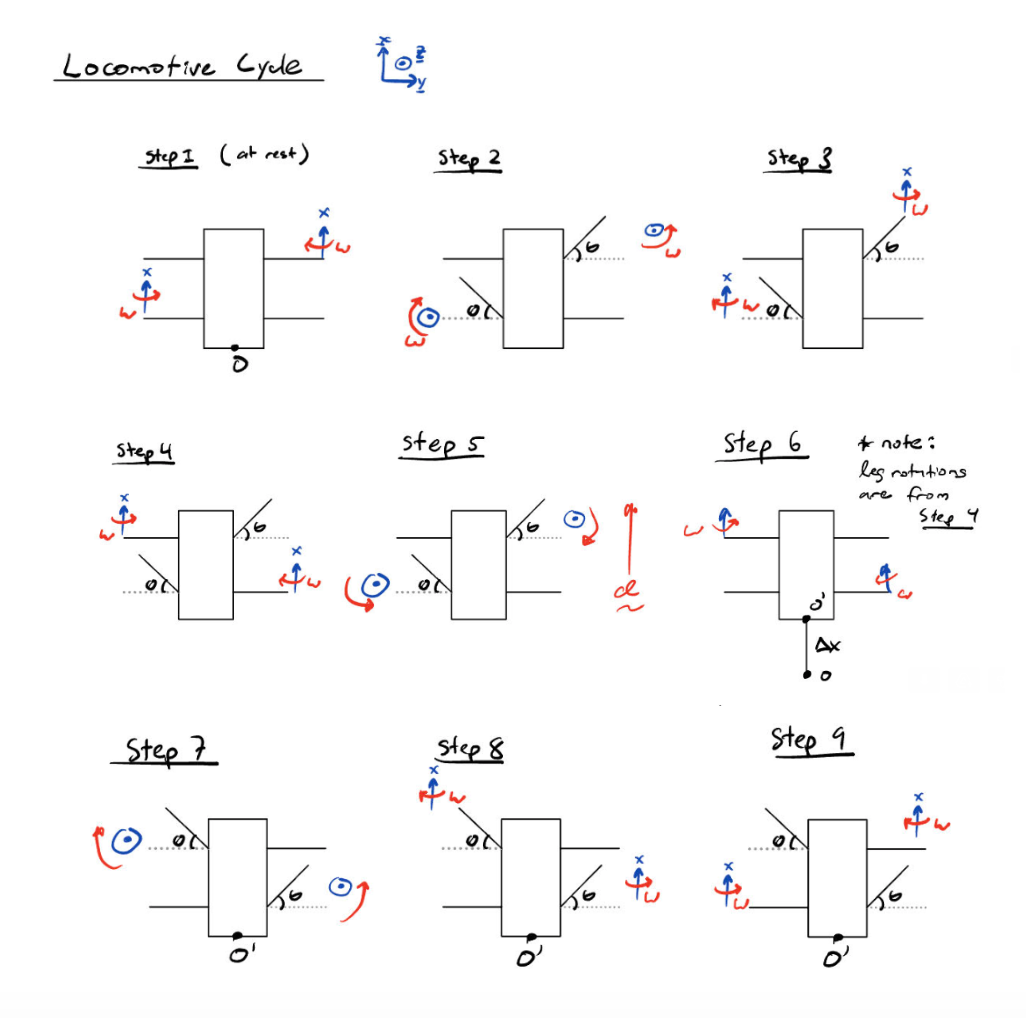
We decided to slightly modify the diagonal gait by extending and pulling back all four legs of the robot at the same time, which would ensure that our CG did not shift away from our desired path. To confirm the stability of this gait we began by analyzing the CG shift and force on CG during regular motion. Assuming a limb length of L, and individual limb weights assigned sequentially, we see that in the neutral position, the Y coordinate of the CG can be found as:
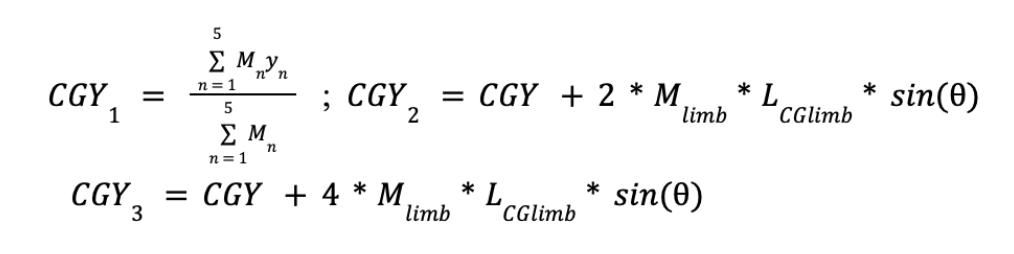
Where theta is the angle with which the limb rotates. Hence we see that as each limb swings forward, the CG shifts slightly forward as well, but due to the symmetry of the robot there is no stray in the X direction. The motion of the gecko with the modified diagonal gait can be summarized as below. The Orange dots represent limb CG and the red dots represent past and present values of system CG.

CAD Model of Design
With all our calculations done, we created our first design iteration, which is shown in Figure 7. Taking the static force analysis conducted above into consideration, we connected the robot’s legs to the underside of its body to minimize the distance between its center of mass and the climbing surface. We also connected the servo for controlling the attachment/detachment of the foot closer to the foot so that less torque would need to be delivered to carry out this movement. The dimensions of the body were 7 inches long and 3 inches wide. The height of the robot’s legs, d1, was 2.5 inches and the length of each leg, d5, was 3.5 inches. The distance between the front and back legs, d23, was 4.5 inches.
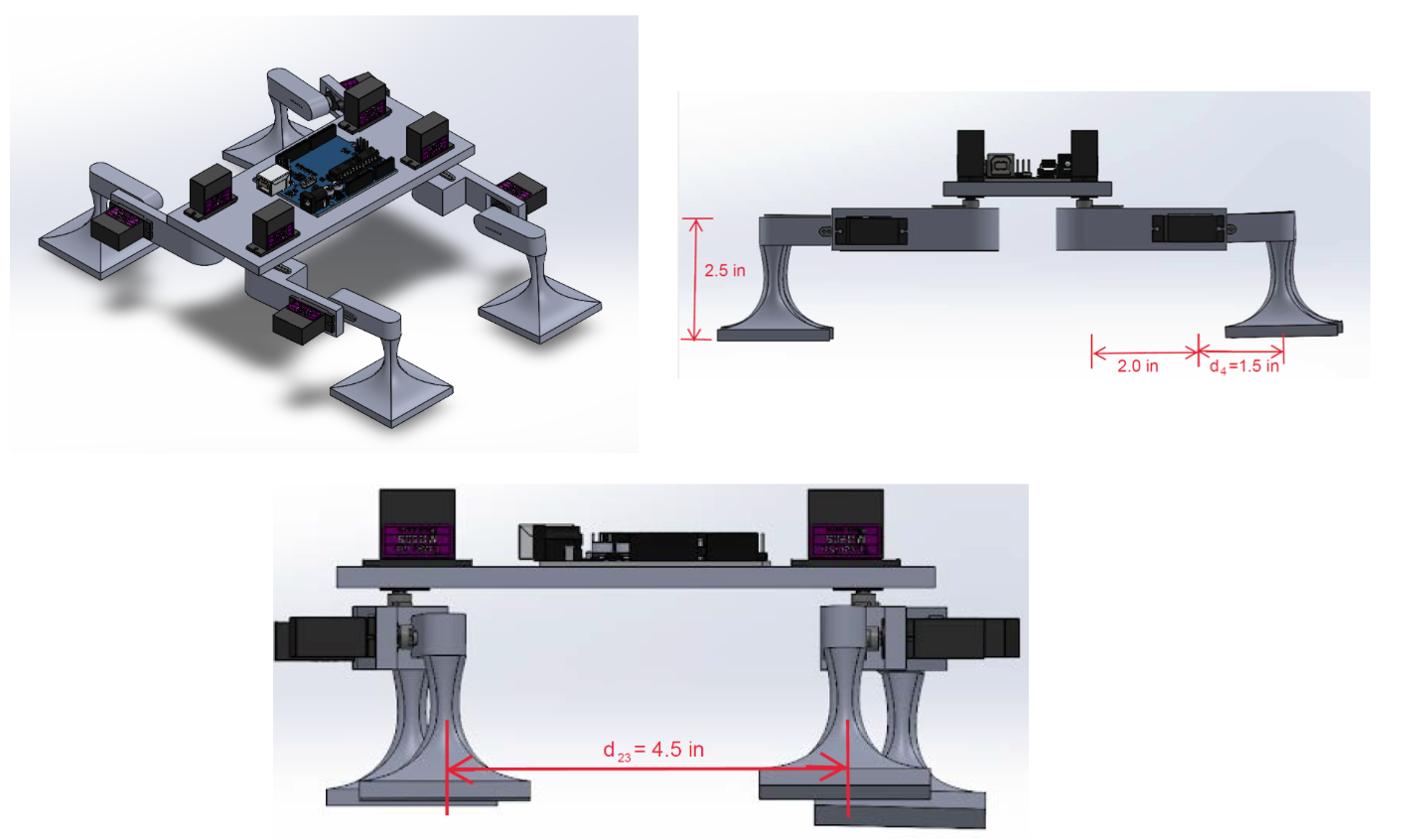
Final Design Iteration
With the 55g servos, the last step remaining was to confirm that the supplied servo torque would be enough to drag the robot forward as seen in the robot locomotive cycle (see figure 6). For this, we performed a basic force analysis on the joints of the robot:
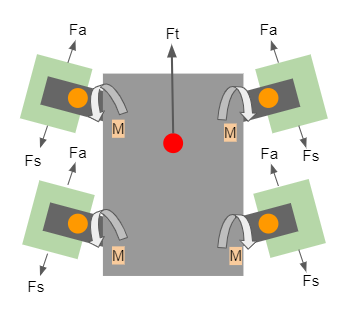
Here Fa is the adhesive force, Fs is the backward force due to the moment M by the servo, and Ft is the net force pushing the body of the GeckoBot forward. For the robot to move, the force of adhesion must be exactly equal to the servo force, such that the pads don't move, which forces the main body to move instead. Assuming a limb length L, we see that:
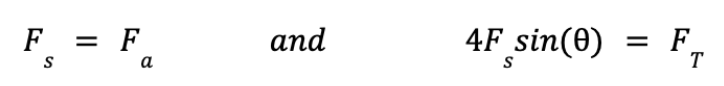
When the robot is perfectly horizontal. When the robot is on an incline of angle phi, then an additional W*sin(phi) component also acts in the downward direction, and the adhesive force must be modified as:
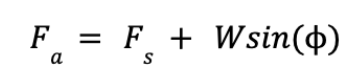
Since we did not implement lamellae, our adhesive force was angle independent as was estimated at a constant value based on physical testing. Hence, this constant adhesive force became a limiting factor in the maximum angle phi the robot could climb, and we found that the supplied servo torque was more than sufficient for efficient horizontal movement and measurement of inclined locomotion. Given the torque rating of 12 Kgcm at 6V for each of the leg servos, we found the net forward thrust force provided by all servos to be 4 times the system weight. Based on previous research, the average required forward force is 71% of body weight when climbing vertically [12], so having the large force margin was desirable as it allowed us to focus on the performance of the gecko inspired adhesive.
Results
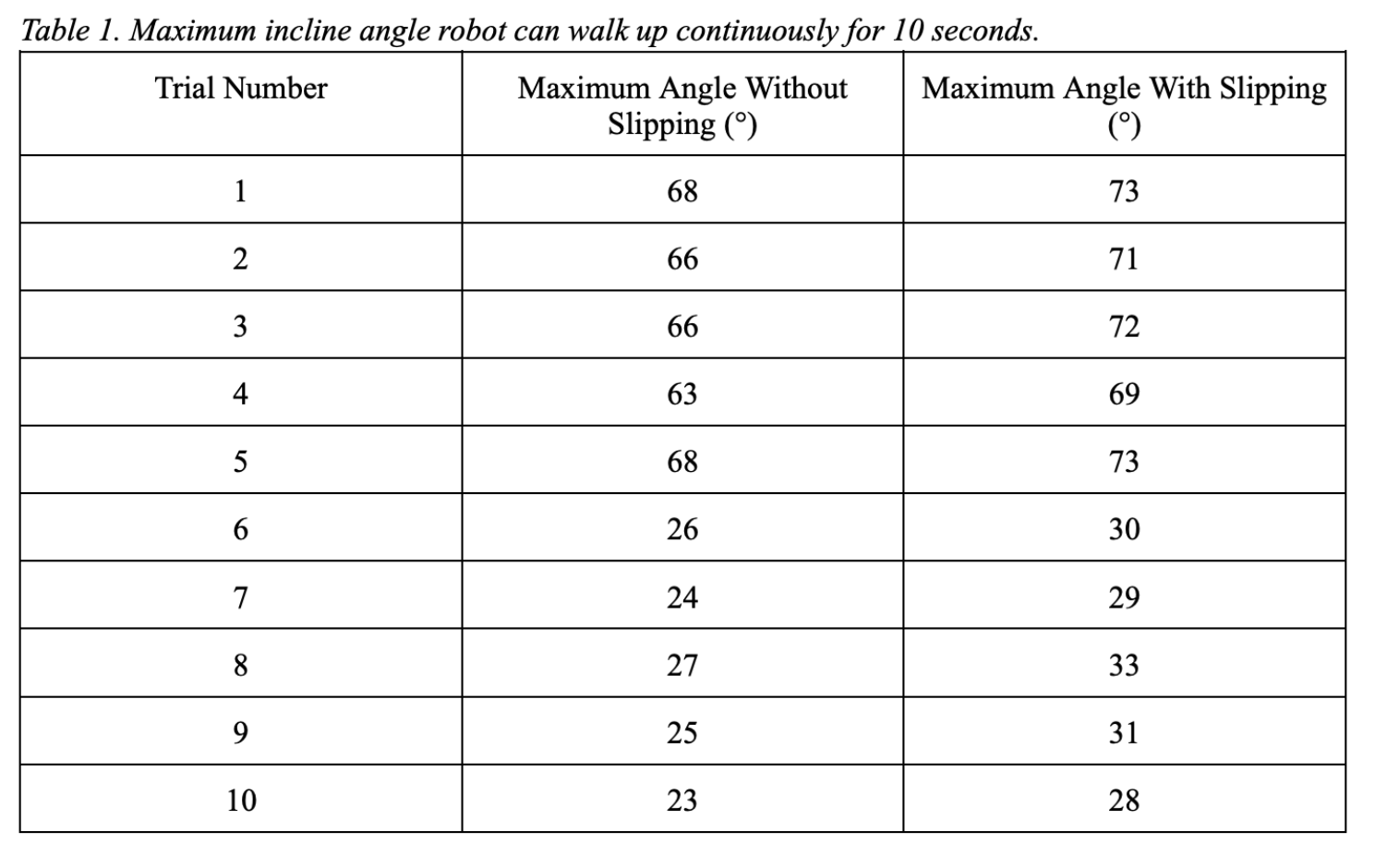
Tests were conducted on an inclined, clean white board. We initially took tests with the robot at rest and with all four of its feet on the white board to ensure the pads were sticky enough to adhere to inclined surfaces. It was determined that the robot could adhere to the white board at an average angle of 71.3°. After these initial tests, we conducted a series of five tests to find the maximum incline angle the robot could climb up without slipping and with slipping. The first five tests were conducted on Monday, November 28th and the last five tests were conducted on Tuesday, November 29th. We conducted these tests by placing the robot at the bottom of the whiteboard and letting it walk up the board for 10 seconds. We increased the incline angle by about 2 degrees until its maximum incline angle was reached.

As seen in the table below, the results aligned well with our predicted maximum angle phi. However, we did notice some slippage in the pads even at lower angles, and this was attributed to the manufacturing method of inconsistencies in mold setting and post processing.
Future Improvements
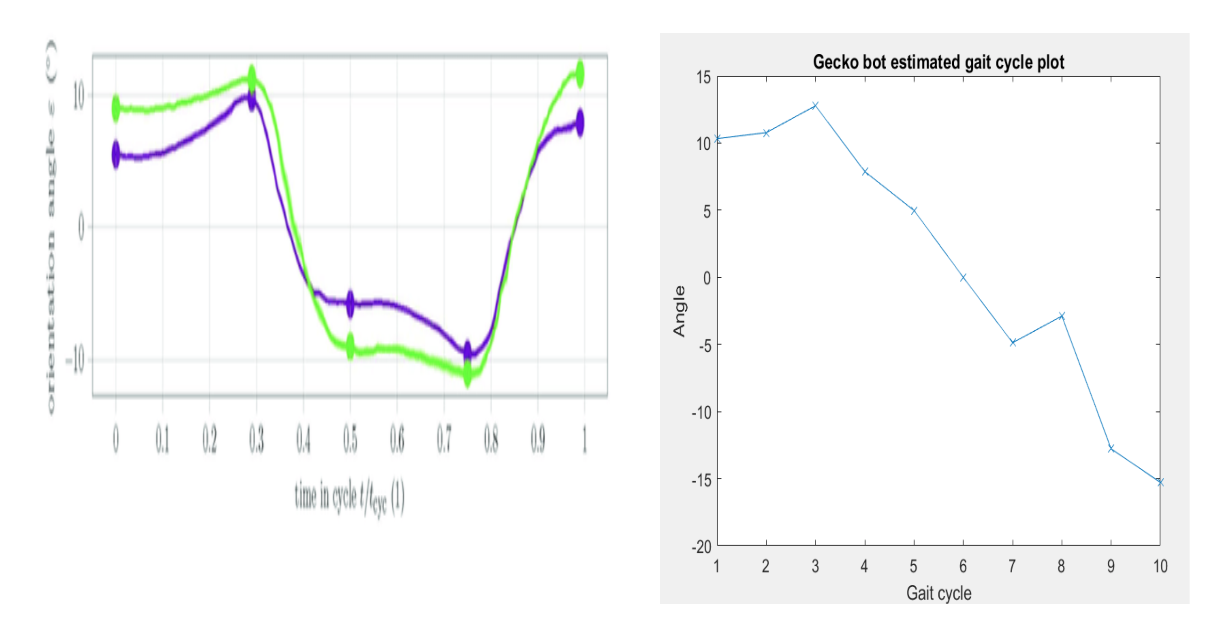
Figure (8) is the estimated gait cycle of our gecko bot and figure (9) is the gait cycle of a gecko according to researchers at the technical university of Hamburg. Comparing the two gait cycles, we can see that our gecko gait cycle initially has a similar trend compared to figure 8. However, the trend quickly becomes different. Our gait cycle explained that we attempted a different method for the locomotion of the gecko as we quickly discovered our limits such as manufacturing accuracy and weight limit would not allow for accurate mimic of gecko movement.
Furthermore, selecting servos that provided sufficient torque while remaining lightweight, such as the Adafruit Micro Servo which would have provided sufficient torque for our robot, would have been possible if we were not subject to budget constraints [9]. Conducting FEA analysis to maintain the stiffness of the design while decreasing the volume of material would have helped minimize the overall mass as well. Research has shown that incorporating a tail in the design of a wall-climbing robot improves the stability and maximum climbing angle of the robot by adjusting the robot’s center of gravity and prevents it from slipping by increasing the friction force between the inclined surface and the robot [10]. Initially we had planned to implement a tail design after developing the first couple of robot prototypes; however, because the weight of our final design was relatively large, it would be detrimental to add additional weight by implementing a tail. If we had successfully kept our robot under approximately 0.5 kg, we would have considered the addition of a tail in our design.
Conclusion
To conclude, our project proved the effectiveness of silicon epoxy in adhering to flat surfaces to drive forward motion in four legged robots. By using higher standards of servo motors and allowing CG shifts in the design to avoid slippage due to CG misalignment we could’ve increased the maximum angle the robot was capable of climbing without slip. Finally, our initial goal mass limit was 0.5 kg whereas we exceeded by reaching 0.98kg. If we could have decreased the mass, potentially our angle of elevation would have been steeper.
References
[1] Tian, Yu, et al. “Adhesion and Friction in Gecko Toe Attachment and Detachment.” Proceedings of the National Academy of Sciences, vol. 103, no. 51, 2006, pp. 19320–19325., doi:10.1073/pnas.0608841103.
[2] Bian, Shiyuan, et al. “A Novel Type of Wall-Climbing Robot with a Gear Transmission System Arm and Adhere Mechanism Inspired by Cicada and Gecko.” Applied Sciences, vol. 11, no. 9, 2021, p. 4137., doi:10.3390/app11094137.
[3] Lv, Hao, et al. “Fabrication of Biomimetic Gecko Setae by Direct Photolithography and Micromolding Processes.” 2011 6th IEEE International Conference on Nano/Micro Engineered and Molecular Systems, 2011, doi:10.1109/nems.2011.6017403.
[4] MENG, Cai. “Design and Analysis of Gecko-like Robot.” Chinese Journal of Mechanical Engineering, vol. 24, no. 02, 2011, p. 224., doi:10.3901/cjme.2011.02.224.
[5] Servo Motor Data Sheet, education.ti.com/html/webhelp/eg_innovator/en/content/eg_innovsys/m_io-datasheets/io_ds_servomotor.HTML.
[6] Amador, Guillermo J., et al. “Soiled Adhesive Pads Shear Clean by Slipping: A Robust Self-Cleaning Mechanism in Climbing Beetles.” Journal of The Royal Society Interface, vol. 14, no. 131, 2017, p. 20170134., https://doi.org/10.1098/rsif.2017.0134.
[7] “MG996R Servo Motor.” Components101, https://components101.com/motors/mg996r-servo-motor-datasheet.
[8] Schiller, Lars, et al. “Toward a Gecko-Inspired, Climbing Soft Robot.” Frontiers in Neurorobotics, vol. 13, 2019, https://doi.org/10.3389/fnbot.2019.00106.
[9] Industries, Adafruit. “Micro Servo - High Powered, High Torque Metal Gear.” Adafruit Industries Blog, https://www.adafruit.com/product/2307?gclid=Cj0KCQiA1sucBhDgARIsAFoytUuL-xewzdeicIqoky6bub1VucrNR6QIf0aFgOKuoupCe8YrPydtfV8aArzVEALw_wcB.
[10] Zang, Guangyuan, et al. “The Roles and Comparison of Rigid and Soft Tails in Gecko-Inspired Climbing Robots: A Mini-Review.” Frontiers in Bioengineering and Biotechnology, vol. 10, 2022, https://doi.org/10.3389/fbioe.2022.900389.
Contributions
Contributions:
Analysis, Diagrams, and Theoretical Model Creation: Nayesha Gandotra and Brittany Navailles
Gecko Pad manufacturing and Testing, Locomotive cycle research: Pablo Alvarez
CAD design and prototyping: Alex Topp
Locomotive Cycle coding and Arduino implementation: Nayesha Gandotra and Seong Ho Yang